人気女性アイドルグループ「TO-NA」のメンバー・スズカは算数・数学が苦手。TO-NA特別アンバサダーのタテルは、そんなスズカの算数嫌いを克服させるというミッションを課された。タテルは別人格「五本松タテル」として、スズカに当たり強めで接しながら、算数・数学の面白さを伝える。

宮崎でのライヴを終え羽田空港へ戻ってきたTO-NAの一行。メンバーの多くが到着ロビーで買い物に勤しむ中、単独行動を好むスズカは上階の出発ロビーに上がっていた。一方、スケジュールの都合で東京に残っていたタテル(ふつうのすがた)はメンバーの到着を待ち構えていた。
「あれ、スズカはどうした?」
「なんかお腹が空いたとか言って上へ行きました」
「宮崎出る前みんなでお昼ごはん食べたのに、まだ食べる気みたいで」
「気儘だね。そうだ俺も昼飯食べてなかったな、スズカを捕まえて食べに行くわ」
タテルは五本松のすがたにフォルムチェンジし、スズカに電話をかける。
「おいスズカ、君が1人出発ロビーにいることはわかってるからな」
「びっくりさせないでくださいよタテルさん」
「君はいけない子だな。今から算数教室を始めるぞ」
「嫌だ!ゆっくり食事させてください」
「どこで食べるか決めているのか?」
「決めてないです」
「俺は今北ウイングゲート外の端にいる。スズカはどこにいる?」
「南ウイングゲート内の端ですね」
「ざっと630m離れてるな。よし、スズカは時速4kmで歩け。俺は時速5kmで歩く。何秒後に俺らが出会うか計算しろ。ただしスズカがゲート外に出る時間は無視する」
「無理ですよ。どう解くんですかこれ」
「それくらい自分で考えなさい。さもなければメンバーの元に戻れ」
「速さ時間距離ってどこをどうかければ良かったんでしたっけ」
「そこからかよ。じゃあそれ思い出しながら歩いてこい。出会ったところで答え合わせだ」

2人が出会った場所にあったのは、羽田空港で人気のカレーうどん店「cuud」であった。席数が比較的多く、中途半端な時間帯であったため行列は発生していなかった。
「カレーうどんだ!美味しそう〜」
「スズカ、その前に答えを言いなさい」
「あそうだった、えーっと、…」
「何も考えてなかったのがバレバレだ。カレーうどんは食べさせません」
「ひどいですタテルさん」
「そもそも君は昼飯を食べているだろう。これ以上食べたら君はどんどんオタフクになってしまう」
「余計なお世話ですよ」
「とにかく!時間は速さと距離をどうすれば求められる?」
「速さと距離をかける!」
「はい残念。君はこれ以上車の仕事をしないように」
「車大好きなのに!」
「なら何故はじきの計算ができない!いいか、まずは3つの要素の単位を考えてみろ。まず距離は630”m”だな。次に時間は?」
「”秒”ですかね」
「じゃあ速さの単位は?」
「車の速度メーター思い出して…”km/h”ですね」
「その通りだ。よく見てみろ、これは分数の形になってる。分数とはつまり割り算だ」
「ちょっと待ってください、分数が割り算?」
「そんなこともわからないのか⁈君はさっさとお嫁に行きなさい」
「問題発言ですよそれ」
「分子を分母で割る。上を下で割る。それが分数というものだ。つまり距離を時間で割ったのが速さ、というものだ」
「なるほど!」
「逆を辿れば、速さに時間をかければ距離となる」
「その逆の辿り方が分からないんですけど。当たり前に言わないでください」
「面倒な奴だ。仕方ない、今日のところはこれ使うしかないな。本当は嫌なんだけど」
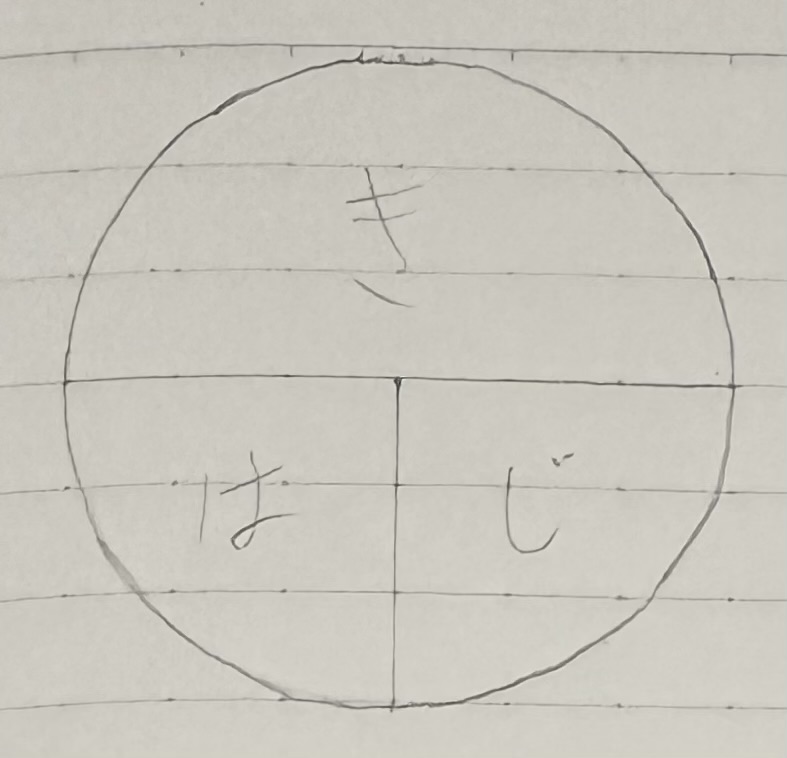
そう言ってタテル(五本松のすがた)は円盤を取り出す。
「上に『距離』、下に『時間』と『速さ』を並べた。求めたいものを手で隠し、残った2つが上下関係にあれば上を下で割ったもの、左右関係にあれば2つをかけたもの、が求めたいものになる。じゃあ問題だ。時速4kmで630mの道を歩くのに要する時間はいくらだろう」
「時間を隠して、距離÷速さだから、630÷4で…」
「これだから円盤使いたくなかったんだ!」
苛立ったタテル(五本松のすがた)は中心をスズカの頭頂部に目掛けて円盤を振り下ろした。
「痛っ!何するんですかパワハラですよ」
「暴力ではない。この円盤は○×どろんこクイズでも使用されている柔らかい発泡スチロール製だ」
「羽田空港のど真ん中でバラエティやらないでください!」
「待った、取らないでその円盤。ヤドキングの首飾りみたいで可愛い」
「恥ずかしいですよ人前で!私はあなたのおもちゃじゃありません!」
「愚か者は便利なものを手にするとすぐ思考停止する。ひみつ道具を手にしたのび太くんじゃないんだからきちんと考えなさい」
「あ、mとkmをどちらかに統一しないといけないのか!」
「時間の方もだ。秒か時間か、どっちに合わせればいいかな?」
「mと秒に合わせます」
「その通りだ。じゃあ時速を秒速に変えろ。時速は1時間で進む距離、秒速は1秒で進む距離のことだ」
「えーっと、1kmは1000mでしょ。だから4kmは4000m。で1時間は60分、1分は60秒、60に60をかけて………3600秒」
「時間かけすぎだ。1時間で4000mということは、1秒だと?」
「4000÷3600でしょ…」
「答えは分数で表すことだな」
「10/9、ですね」
「やっと結論出たよ。じゃあ店入るぞ。あ、単位はm/sね」
まずは食券を買うのだが、席が空いているかどうかを視認できず、店員の声かけも遅かったため買うタイミングに迷ってしまう。ちなみに行列ができている場合は、席が空いてから食券を購入する。
それでも店内に入った途端出汁の香りが2人の鼻を刺激し期待感を膨らませる。
「漸く本題に入れる。南北に走る全長630mの一本道を、スズカは南端から時速4kmで、俺が北端から時速5kmで歩くとき、俺らは何秒後にどの地点で出会うだろうか」
「私は秒速10/9m、タテルさんは5000÷3600で…秒速25/18m。だからなんでしょう…」
「分からなければ図を描け。そして法則性を見出してみろ」

「1秒でこれだけ進む、2秒でこう、3秒で…」
「カレーうどんは茹で上がり早いぞ。早く法則見つけて計算始めろ」
「法則なんて言われてもわからないよ〜」

結論を出すことができないまま、カレーうどんが着丼した。

ノーマルのカレーうどんはスパイスがよく効いていてインドカレーのようである。細麺によく絡み、濃厚さもあってかなり美味しい。

トマトカレーうどんは一転お出汁の香りが強い。出汁のうま味とトマトのうま味が仲良しこよししている。
「哀れだが答えを教えるしかない」

1秒でスズカは10/9m、俺は25/18m進む。それぞれ紫と赤の帯で図示した。縮尺がちょっとおかしいのは見やすくするための処置だから気にしないでくれ。この赤帯を紫の方に寄せてみると、630mの道のりの内5/2(=2.5)mが埋まったことになる。つまり1秒で2人合わせて2.5m進む。2秒で5m、3秒で7.5m。これが丁度630mになった時、それが2人の出会う時刻となる。
「1秒で2.5mだから、式はどうなる?」
「え?えーっと…」
「単位量の計算もできないのか。君はやはりお嫁に…」
「不適切ですよ!630÷2.5で、答えは…」
「63×4をすれば良いだろうに。答えは252秒、つまり4分12秒だ」
「最後まで計算させてくださいよ」
「遅すぎる。それじゃ東大合格なんて夢のまた夢だ」
「目指してません」
「目指すかもしれないじゃないか、君の番組でMCやってる後楽園氏みたいに」
「あり得ないです」
「あり得ない?あり得ないなんてことはあり得ない」
「言わせちゃったよ…」
カレーうどんは出汁を入れて味変をすることができる。ノーマルよりトマト味の方が、トマトと出汁双方の持つ旨味成分の相乗効果のおかげか美味しく味変ができる。
2人の元へ、TO-NAメンバーのヒヨリからLINEが届いた。
みんなもう買い物済ませてしまいましたよ。私とヒナはこれからタクシー乗り場に向かうので、2人も早く来てください!
「ヒナちゃ〜〜〜〜〜ん!」
「どうしたんですかタテルさん」
「見てんじゃねぇよ!」
「こわ〜い!」
「ヒナちゃんとヒヨリはのんびり屋さんだから時速3kmで歩くだろう。僕らは時速7kmの速歩きで追いつくぞ」
「結構速くないですか⁈」
「僕のデフォは7kmだ。そうでないと科学者なんぞやっていけない」
「だから私違いますって!」

僕らのいる地点から105m先にあるショッピングエリアからヒナちゃん達が出発する。そこからタクシー乗り場まではさらに70m先だ。全員同じタイミングで歩き出した場合、さっき言った条件で、俺らはヒナちゃん達に追いつけるだろうか?追いつけない場合、何秒遅れで僕達はタクシー乗り場に到着するだろうか?
「時速3kmは秒速に直すと、3000÷3600だから…秒速5/6m」
「スズカくん、こういう時は後先考えろ。時速7kmの方は?」
「…秒速35/18mですね」
「分母が揃ってない。時速3kmの方は最後まで約分せず、15/18で止めておくと二度手間にならず済む。まあいいや、じゃあ追いつき算を解け」
「まずは図を描いてっと。…2組の距離の差は105m、速さの差は秒速20/18m…」
「そこは約分しようぜ。気持ち悪い」
「ごちゃごちゃうるさいです!

秒速10/9mだから…差が1秒で10/9m縮む訳だ!105mの差を埋めるには105を10/9で割る。分数の割り算は…」
「遅い。9/10、すなわち0.9をかけて94.5秒だ。一方ヒナちゃ〜んの一行は秒速35/18mで70mの道を歩く訳だから、70×18/35=36秒で着いてしまう。頑張って歩いても、僕達の方が58.5秒遅れてしまう。スズカくん、58.5秒遅れるってヒナちゃ〜んに伝えておいて」
「細かいですね、1分でいいじゃないですか」
「良くない。1.5秒あれば早押しクイズでボタン押して正解できる」
「それに何ですか『ヒナちゃ〜ん』って呼び方。気持ち悪いんですけど」
「何が悪い」
「全部悪いです!早く追いかけましょうよ!」
「ヒナちゃ〜ん!」
「ど、どうしたんですかタテルさん」
「ヒナちゃん、あなたの知ってるタテルさんとは別人だからね」
「どういうこと?」
「余計なこと言わなくていいからねスズカくん」
「もう、いけずなんだから…」
「ヒナちゃん、帰ったら一緒に『NINZABURO FURUHATA3』第8話観ようね」
「はい!」
「受け入れるの早っ…私も観たいです!」
「ダメだ。スズカくんは宿題をやりなさい」
先程解いた追いつき算において、スズカ達がヒナ達に追いつくためには、スズカ達は時速何m以上で歩く必要があっただろうか。
「何で私だけ…」
「やっぱりスズカの負け顔は最高だ。な、ヒナちゃん」
「そうですね。あ、後でチャーハン作るので食べません?」
「ヒナの作るものなら何でも食べるさ」
「やった!…どうしたスズカちゃん?」
「タテルさん…いい加減にしてください!」
「寝ちゃったねタテルさん」
「もう最悪!」