人気女性アイドルグループ・綱の手引き坂46(当時)のメンバー・スズカは算数・数学が苦手。綱の手引き坂特別アンバサダーのタテルは、そんなスズカの算数嫌いを克服させるというミッションを課された。タテルは別人格「五本松タテル」として、スズカに当たり強めで接しながら、算数・数学の面白さを伝える。
「えーっと、新10000円札は渋沢栄一、新5000円札は津田梅子…」
「何やってんだスズカ」
「タテルさん、私今度クイズ番組に出ることになったんです。だから一般常識を対策していて」
「君がクイズ番組に?物好きなスタッフもいるもんだ」
「バカにしないでください」
「じゃあ問題だ。円の面積を求める公式は?」
「えーっと、あれ?半径だっけ直径だっけ?2かけるんだっけ…」
「阿呆丸出しじゃないか。πr^2だろ。半径×半径×3.141592…」
「3.14じゃダメなんですか?」
「ダメだ。πは無理数だ、どこかで切るもんではない」
「知りませんよ。何なら小数点もいらない、3で計算したいくらいですよ」
「君みたいな大雑把な人とは付き合いたくもない」
「あなたみたいな口うるさい人とは絡みたくないです」
「ああそうですか。せっかく美味いお好み焼き食べに行こうと思ってたのに」
「お好み焼き⁈行きます行きます!」
「単純な奴だ」

土曜日の品川駅港南口。オフィス街の休日はそこまで人が多くなく、食肉市場から漂う断末魔の臭いも無い。駅から徒歩5分ほどの場所にある品川フロントビルの2階に目的のお好み焼き屋がある。
「行列できてますね。何分くらいかかるでしょうか…」
「さあ。客は気まぐれだからな、早く食べる人もいればぺちゃくちゃ喋りながらちんたら食べる周り見えてない輩もいる」
「後半ただの悪口じゃないですか」
「とにかく何分並ぶかは分からない。我慢して待ちなさい」
結局30分程待って入店した。大阪でも有名な店「きじ」の東京支店のひとつ、とあって行列が絶えない店である。

「牛すじ、意外と食べ応えあるな。ポン酢のアクセントで余計酒が進む」
スジポンと円周率をツマミに翠ジンソーダを呷るタテル。
「スズカ、そもそも君が3.14だと曲解している円周率、なにものだと思ってるんだ」
「なにもの、と言われましても…3.14だな、としか思わないです」
「これだからお気楽者は。じゃあ何故円周の長さは2πrなのか」
「誰かが勝手に決めたんじゃないですか?」
「たまにはいいこと言うな」
「えっ?私、正解言いました?」
「ああ。円の直径に円周率というものを掛けたら円周の長さになる、っていう取り決めに先人がしたんだ」
「へぇ〜」
「このように、誰かが勝手に取り決めたルールを『定義』という。(直径)×(円周率)=(円周)は『定義』だ。何故そうなる、と訊かれても、そう取り決めたから、としか言えない」
「なるほど。誰かさんが円周率とはこうであると定めて、私たちもそれに乗っかっているわけですね。でもなぜ円周率が3.1415…という値になるとわかるのでしょうか」
「どうやると思う?」
「ノーアイデアです」
「諦めるの早いな。正解したら東大生レヴェルだ、って褒めてあげようと思ったのに」

そこへ最初のお好み焼きがやってきた。ネギと鶏皮を入れ、ポン酢で味を決めた店長おすすめ焼。ヘラを手にしたタテルはお好み焼きの周をなぞるように先端をなぞった。
「何をしたいんですか?早く切り分けましょうよ
「ヘラの幅6個分の長さか。このヘラの幅は10cm、だから円周の長さはざっと60cm」
「鶏皮の脂とカリカリ、そこへポン酢の酸味も加わりデリシャスズカ!」
「話を聞け!これが円周率のおおよその値の求め方だ」
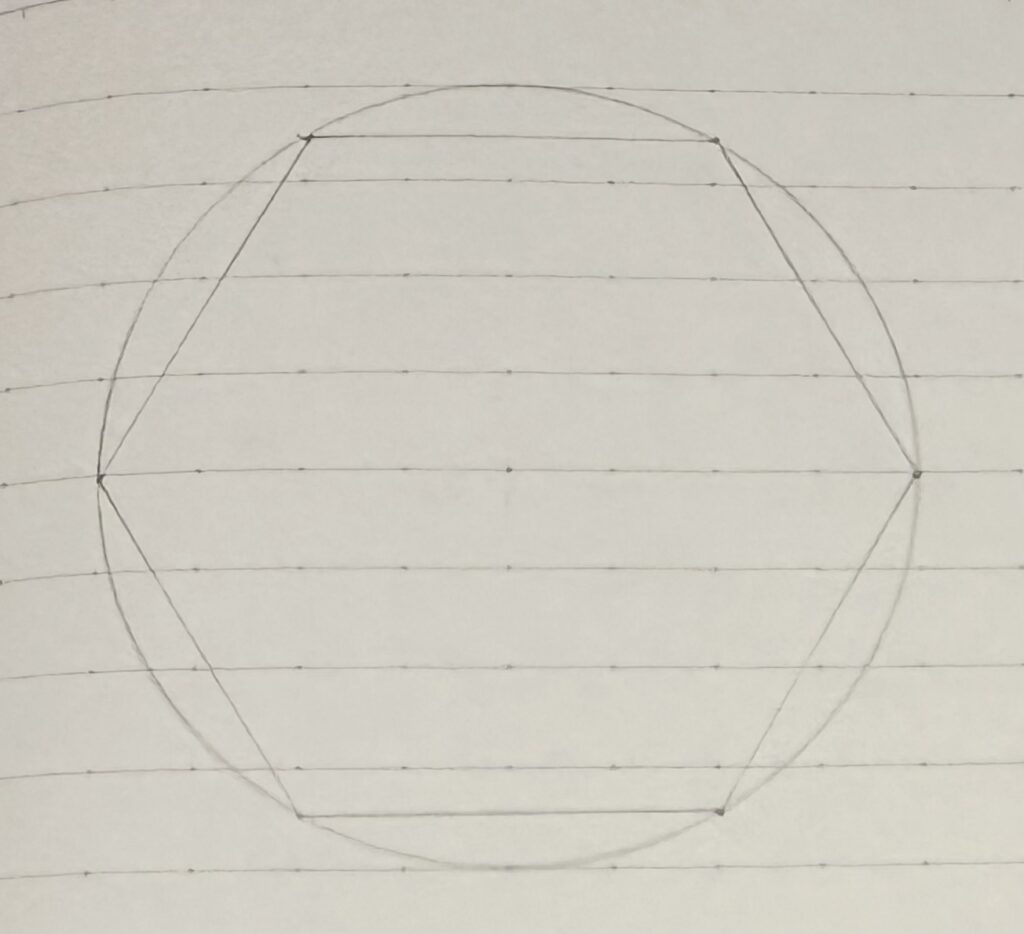
全ての頂点が同一円周上にある正多角形、通称「円に内接する正多角形」を考える。その周の長さは三角比を使えば容易に求められる。今回は正六角形にしてみよう。正六角形なら算数の範囲内で周の長さがわかる。円の半径を1とすると、周の長さは?
「なんとなく1辺の長さが1な気がするので、周の長さは6?」
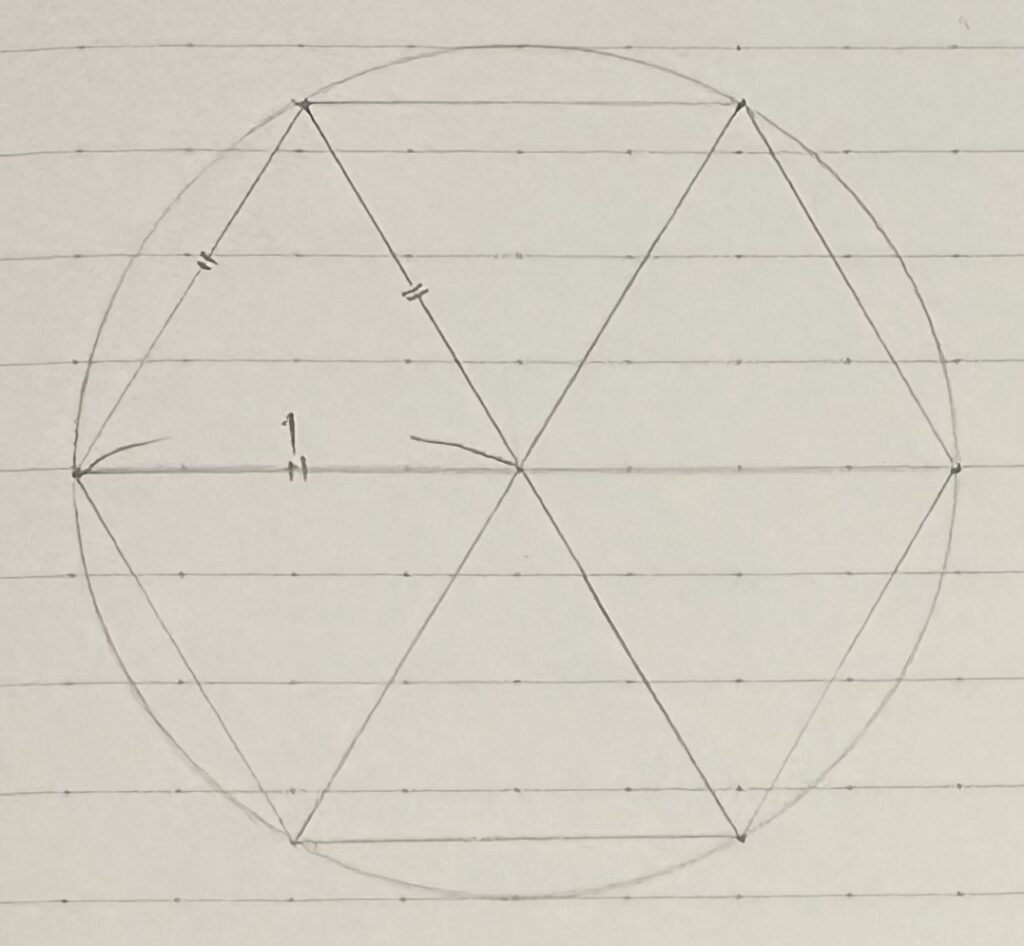
何となく、は嫌いだが答えはそうだ。ちゃんとした導き方は宿題にするとして、正多角形の周の長さは6、一方で円周の長さは2×円周率。円周の方が長いから、円周率は3より大きいといえる。
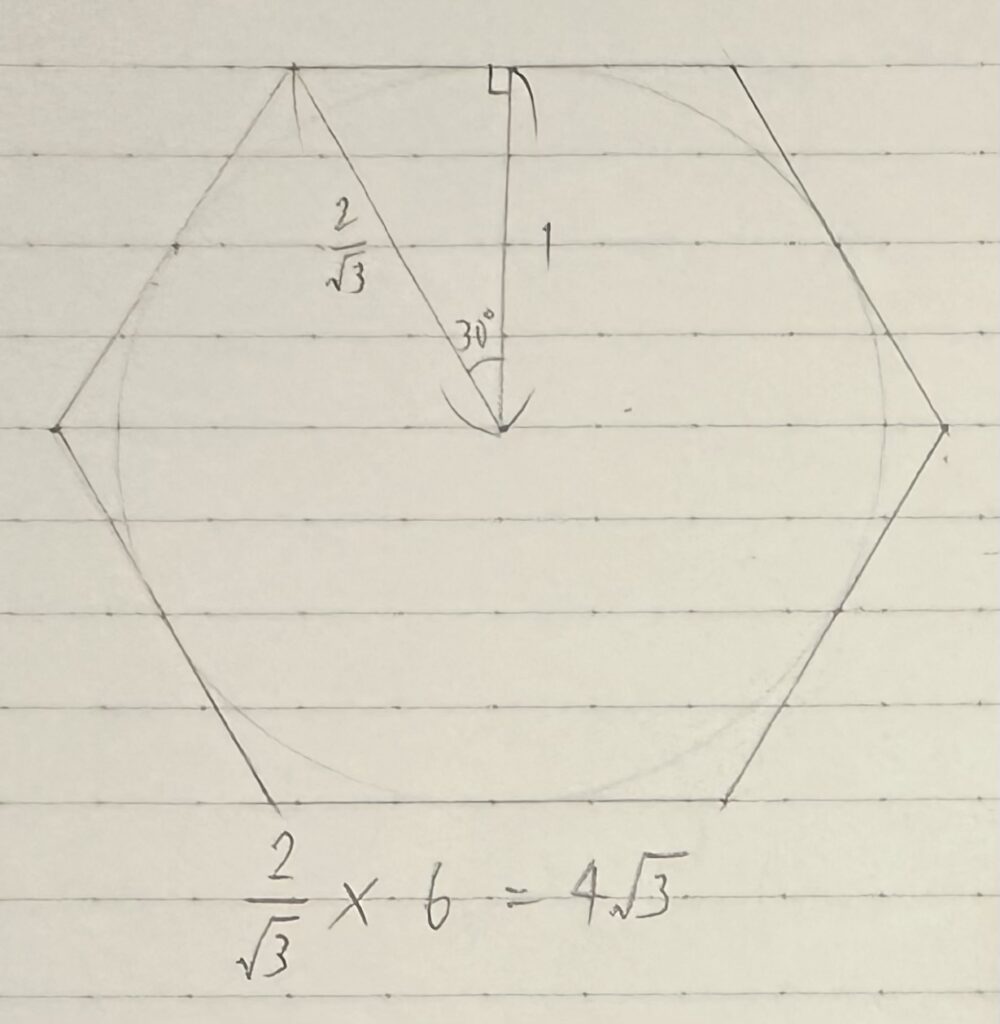
今度は各辺が半径1の円に接する正六角形、つまり「円に外接する正六角形」を考えよう。こちらは正六角形の周の方が円周より長い。三平方の定理を使う必要があるから中学の範囲になるが、円周率が2√3=3.464…より小さいことがわかる。
「今回は正六角形で考えたが、角の数を増やしていけば精度が上がる。正多角形も角を増やせば円みたいになるのは感覚でわかるだろ?」
「そうですね。って、あれ?タテルさんが珍しく感覚で語ってる」
「初学者に対してはある程度の妥協が必要だ。算数嫌いのスズカに対しては尚更ね」
「結局バカにしてるじゃないですか」

続いて定番の豚玉が登場。タテルはそれを扇形に8等分すると、そのうち4つを、尖った方を上にして横に並べ、隙間を埋めるように残り4つを上からはめた。
「タテルさん、食べ物で遊ばないでください。早く食べたいんですけど」
「君が円の面積を求める公式を間違えるからだ。わかりやすく説明しようと思ってこうした」
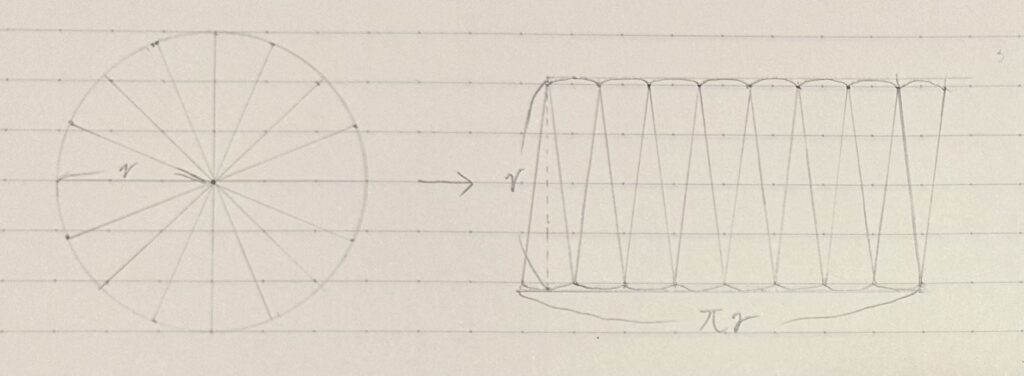
こうやって円を扇形に等分し、互い違いに配置すれば平行四辺形みたいな図形になる。もちろん底辺が波線みたくなっているから完璧な直線では無いが、底辺×高さとしておおよその面積を求められる。高さは円の半径、底辺は円周の半分だから円周率×半径。したがって面積は(半径)×(半径)×(円周率)である。
「これも扇形を細かくしていけば精度は高まる。がやはり感覚ではあるかな。無限に細かくすれば円の面積に一致するが、その『無限』というものに実体は無い」
「無限とはマボロシみたいなもの、まさしく『夢幻』ですね」
「何言ってるかわかんない。罰としてスズカには、底辺の波線を直線にした時の切れ端だけあげよう」
「嫌ですよ!がっつり食べさせてください」
キャベツの甘みなどはたしかにあるが、お好み焼きに愛着の無いタテルはすぐ飽きてしまった。
「やっぱり全部あげる。ソースの味、濃いけどもっと深みが欲しい」
「文句が多いですね」
「俺はソースの濃さを流す酒をもらう。林檎梅とは珍しいな」
「1人2枚いけるかと思ったけど無理だな」
「タテルさん欲張りすぎですよ」
「いけると思うじゃん」
「タテルさんでも予測見誤るんですね」
「うるさい。俺は江戸っ子だい、もんじゃの方が好きだ」
「じゃあなんでお好み焼き屋さんに来たんですか?」
「もんじゃでは今日みたいな解説ができないからだ、それくらい察しなさい。じゃあ宿題だ」
①半径1の円に内接する正六角形の1辺の長さが1であることを示せ。
ヒント:二等辺三角形を見出せ
②先ほどは扇形に分割したあと四角形を作って面積を求めたが、扇形を全て横に並べても、ある変形をすれば一発で(半径)×(半径)×(円周率)が導き出せる。どうすれば良いだろう。
ヒント:高さは同じ
「ちなみに円周率は3.1415926…と無限に続き、数字の出現パターンも完全ランダムだ。こういうのを無理数と言う。終わりの無い円周率を100万桁も書き連ねた本があってな」
「随分と物好きな方ですねそれ書いた人」
「それでも終わりじゃないからな。無理数は終わらない。だから円周率も終わらない」
「終わらないって響き、なんか素敵ですね」
「だろ。円周率とはそれだけ神秘的なものなんだ。もし君が将来結婚式を挙げて俺を招待してくれたら、永遠を祈願してご祝儀にはπ万円包んでおくよ」
「待ってください、π万円なんてどう用意するんですか」
「その辺の紙にπ万円って記して…」
「ふざけないでください。やっぱりバカにしてる」
「ネイピア数でもいいぞ。πと双璧を成す神秘的な無理数、e=2.718…」
「安心してください、タテルさんなんか招待しませんから」
「この恩知らずが」
「恩なんかもらってませんから。早くふつうのタテルさんに戻ってください」
「知らないな」
「めんどくさい…」
NEXT